二叉树介绍
二叉树_百度百科
二叉树由一个个节点构成,最上方是根节点,一个节点可能有它的左节点和右节点,由左节点作为根节点的树叫做左子树,由右节点作为根节点的树叫做右子树。
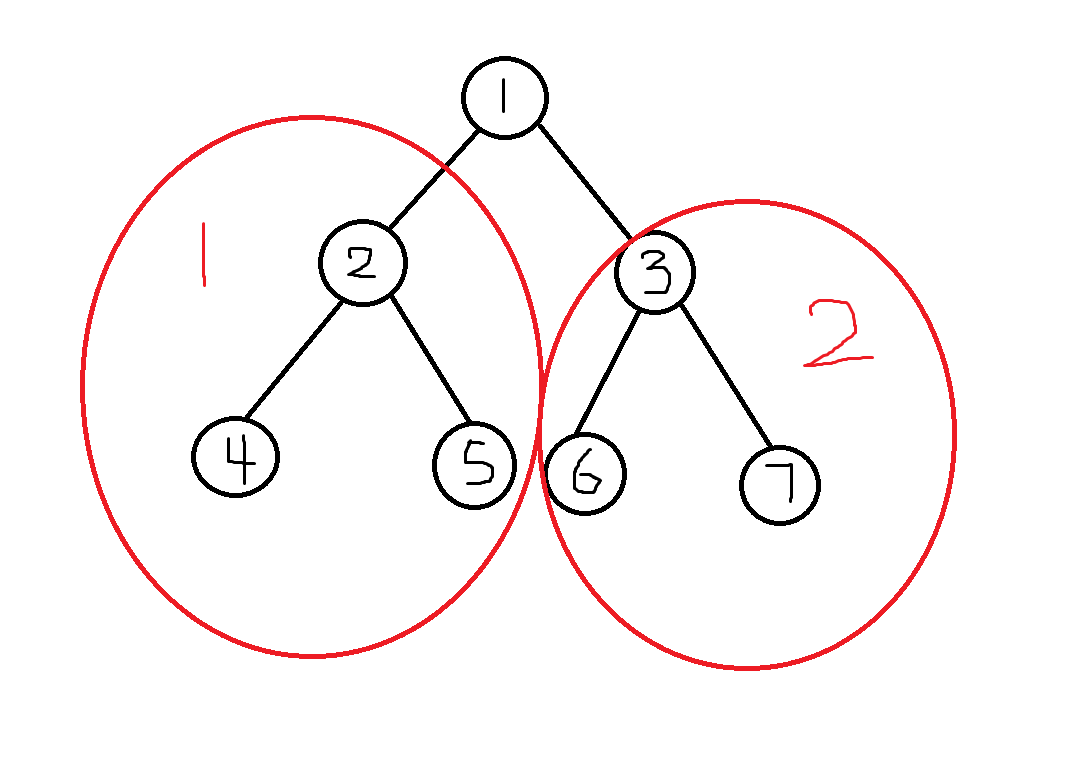
如图为一颗有七个节点的二叉树,节点1便是这颗树的根节点,而红圈1为根节点的左子树,红圈2为根节点的右子树。
如何描述一颗树
除了像这样直接画一张图出来,如何描述一颗树呢?
描述节点的对应关系:比如,直接叙述节点1为根节点,2和3分别为1的左子树和右子树。再描述2的左子树和右子树有等等。
这样直接叙述固然可行,下面给大家介绍几种常见的遍历树的方式。
层序遍历
即按照每层描述这颗树的元素。自上而下,自左而右。
按照上图,该树的层序遍历为:
前序遍历
从根节点开始,按照由节点本身,左节点,右节点的形式输出值。如果该节点有左子树和右子树,也按照该顺序。
按照上图,该树的前序遍历为:
中序遍历
从根节点开始,按照由左节点,节点本身,右节点的形式输出值。如果该节点有左子树和右子树,也按照该顺序。
按照上图,该树的中序遍历为:
后序遍历
从根节点开始,按照由左节点,右节点,节点本身的形式输出值。如果该节点有左子树和右子树,也按照该顺序。
按照上图,该树的后序遍历为:
注意
这四种遍历方法中,仍给两种遍历方法,可以帮我们得到一颗确定的树。
建树
在我们的代码中如何表示出一棵树?
我们先来想想每个节点的特性,首先,每个节点自身都有一个值,然后它可能有左节点或者右节点。(如果这个节点既没有左节点,也没有右节点的话,那么这个节点被称为叶子节点。)那么我们可以用一个结构体来表示每个节点。
1
2
3
4
5
6
| struct Node
{
Node * left,* right; // 左节点的指针和右节点的指针
int value; // 本身的值
Node():left(NULL),right(NULL){}; // 初始化左节点和右节点为空
};
|
由于我们不清楚树的大小,因此我们对于每个节点都采用动态添加的方法。这个时候就要用到 new 和 delete 关键字。new可以动态申请一个内存用于对应的节点,delete可以删除(或者说归还更合适一点)掉申请的内存。
因此,我们可以这样直接新建一个节点。
1
2
3
4
| Node * newnode()
{
return new Node();
}
|
那我们就可以这样构建一棵树。
1
2
3
4
5
6
| Node * root = newnode(); // 构建根节点
root->value = 1;
root->left = newnode(); // 构建根节点的左节点
root->left->value = 2;
root->right = newnode(); // 右节点
root->right->value = 3;
|
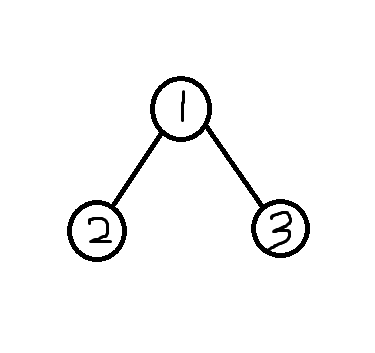
建出的树如图。
dfs
那么我们如何遍历这颗树?以前序遍历为例。
1
2
3
4
5
6
7
| void dfs(Node * root)
{
cout << root->value << " ";
if(root->left!=NULL) dfs(root->left);
if(root->right!=NULL) dfs(root->right);
return;
}
|
这种遍历方式被称作深度优先搜索。通常使用递归的方式实现,既然是中左右的顺序,那么拿到一个节点,就立马输出这个节点的值,然后再递归的去搜它的左节点和右节点,直到搜完为止。
我开始遍历的方式便是:
同样的,我们的delete操作也可以用dfs的形式来写。
删完它的左右节点,再删他本身。
1
2
3
4
5
6
7
| void remove_tree(Node * u)
{
if(u==NULL) return;
remove_tree(u->left);
remove_tree(u->right);
delete u;
}
|
bfs
曾经的博客中我介绍了stl的相关内容,那么借助queue队列,我们可以实现层序遍历。自上而下,自左而右。
1
2
3
4
5
6
7
8
9
10
11
12
13
| void bfs(Node * root)
{
queue<Node *> q;
q.push(root);
while(!q.empty())
{
Node * cnt = q.front();
q.pop();
cout << cnt->value << " ";
if(cnt->left!=NULL) queueTree.push(cnt->left);
if(cnt->right!=NULL) queueTree.push(cnt->right);
}
}
|
首先把第一层的元素扔进队列,也就是根节点,然后依次添加左节点,右节点,左节点再添加左节点右节点。
根据队列的特性,就可以实现自上而下,自左而右地访问到每一个节点。
这种遍历的方法被称做广度优先搜索。
例题
uva122
题目链接:Trees on the level - UVA 122 - Virtual Judge
题意
题意不难理解,即为先建树,再按层序遍历输出元素。
难点解析
- 每个输入的格式显得有些难以处理
- 如何判断是否存在重复节点?
- 如何判断必要节点不存在?
让我们挨个解析
难点1:输入处理
让我们以(7,LLL)为例。
我们从这个字符串中至少应该获取到两个数据,即节点的值和表示位置的字符串,那么我们可以用到string类自带的find函数和substr函数。
find函数可以查找到需要查找的字符在字符串中的位置(从0开始)
substr函数的第一个参数为子字符串开始的位置,第二个参数为需要截取的长度,因此,我们可以搜索,的位置,然后分别截取即可,示例代码如下
1
2
3
| // nodeTen为类似(7,LLL)的结构
nodeTen.substr(nodeTen.find(',')+1,nodeTen.length() - nodeTen.find(',') - 2) // LLL
atoi(nodeTen.substr(1,nodeTen.find(',')-1).c_str()) // 7
|
难点2:判断节点是否重复
在node结构体中添加一个bool类型的变量用于记录之前是否赋值过即可。
难点3:判断必要节点不存在
深搜或广搜一遍树,如果存在节点未被赋值,则说明必要节点不存在。
示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
| #include <iostream>
#include <queue>
using namespace std;
struct Node
{
bool haveValue;
Node * left,* right;
int value;
Node():haveValue(false),left(NULL),right(NULL){};
};
Node * root = NULL;
Node * newnode()
{
return new Node();
}
void remove_tree(Node * u)
{
if(u==NULL) return;
remove_tree(u->left);
remove_tree(u->right);
delete u;
}
bool addNode(string ten,int value)
{
Node * currentNode = root;
for(int i=0;i<ten.length();i++)
{
if(ten[i] == 'L')
{
if(currentNode->left==NULL) currentNode->left = newnode();
currentNode = currentNode->left;
}
else
{
if(currentNode->right==NULL) currentNode->right = newnode();
currentNode = currentNode->right;
}
}
if(currentNode->haveValue)
{
return false;
}
currentNode->haveValue = true;
currentNode->value = value;
return true;
}
int main()
{
string nodeTen;
while(cin >> nodeTen)
{
remove_tree(root);
root = newnode();
bool flag = true;
flag = addNode(nodeTen.substr(nodeTen.find(',')+1,nodeTen.length() - nodeTen.find(',') - 2),atoi(nodeTen.substr(1,nodeTen.find(',')-1).c_str()));
while(cin >> nodeTen && nodeTen!="()")
{
if(flag)
{
flag = addNode(nodeTen.substr(nodeTen.find(',')+1,nodeTen.length() - nodeTen.find(',') - 2),atoi(nodeTen.substr(1,nodeTen.find(',')-1).c_str()));
}
}
if(nodeTen == "()")
{
if(!flag)
{
cout << "not complete\n";
continue;
}
else
{
bool rightAns = true;
vector<int> ans;
queue<Node *> queueTree;
queueTree.push(root);
while(!queueTree.empty())
{
Node * cnt = queueTree.front();
queueTree.pop();
if(!cnt->haveValue)
{
rightAns = false;
break;
}
ans.push_back(cnt->value);
if(cnt->left!=NULL) queueTree.push(cnt->left);
if(cnt->right!=NULL) queueTree.push(cnt->right);
}
if(!rightAns)
{
cout << "not complete";
}
else
{
for(auto i = ans.begin();i!=ans.end();i++)
{
cout << *i;
if(i!=ans.end()-1)
{
cout << " ";
}
}
}
cout << "\n";
}
}
}
return 0;
}
|
uva548
题目链接
这题很显然符合我们刚刚提到的结论,给出四种遍历方式中的两种,一定可以确定一棵树,自然也就可以输出其第三种遍历。
那么本题中根据中序和后序,我们应该如何建树呢?
以这组数据为例
1
2
| 3 2 1 4 5 7 6
3 1 2 5 6 7 4
|
后序遍历的形式是左右中,也就是说,最后一个子节点一定是这棵树的根节点。
而中序遍历的形式是左中右,也就是说,根节点的左边是左子树的中序遍历,根节点的右边为右子树的中序遍历。
可以得出,左子树的元素个数为3,因为后序遍历以左右中的形式,所以左子树的后序遍历为前三个元素。右子树可以类比。
根据分治的思想,我们就可以如此不断的建树。直到中序遍历和后序遍历都只有一个元素为止。
建树完成,再深搜一遍确定最小值即可。
因此,示例代码如下,代码中用到的方式是以数组的形式建树(用两个数组分别表示对应节点的左节点和右节点是啥)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
| #include <iostream>
#include <sstream>
using namespace std;
int tree_zhong[10001];
int tree_hou[10001];
int lch[10001],rch[10001];
int n;
void loadTree(string cmd,string pos)
{
stringstream s(cmd);
n=0;
int x;
if(pos == "zhong")
{
while(s>>x)
{
tree_zhong[n] = x;
n++;
}
}
else
{
while(s>>x)
{
tree_hou[n] = x;
n++;
}
}
}
int buildTree(int l1,int r1,int l2,int r2)
{
if (l1>r1)
{
return -1;
}
int root = tree_hou[r2];
int p;
for(int i=l1;i<=r1;i++)
{
if(tree_zhong[i] == root)
{
p = i;
break;
}
}
lch[p] = buildTree(l1,p-1,l2,l2+p-l1-1);
rch[p] = buildTree(p+1,r1,l2+p-l1,r2-1);
return p;
}
int sumMin = -1;
int minID = -1;
void dfs(int root,int sum)
{
sum += tree_zhong[root];
if(lch[root]==-1 && rch[root]==-1)
{
if(sumMin == -1)
{
sumMin = sum;
minID = root;
}
if(sum == sumMin)
{
if(tree_zhong[root] < tree_zhong[minID]) //不加这个判断uva也过了
{
sumMin = sum;
minID = root;
}
}
if(sum < sumMin)
{
sumMin = sum;
minID = root;
}
return;
}
if(lch[root]!=-1)
{
dfs(lch[root],sum);
}
if(rch[root]!=-1)
{
dfs(rch[root],sum);
}
}
int main()
{
string cmd;
while(getline(cin,cmd))
{
sumMin = -1;
minID = -1;
loadTree(cmd,"zhong");
getline(cin,cmd);
loadTree(cmd,"hou");
int root = buildTree(0,n-1,0,n-1);
dfs(root,0);
cout << tree_zhong[minID] << endl;
}
return 0;
}
|
uva839
题目链接
这题虽然一眼看上去是二叉树的形式,实际上并不需要建树。
通过对于引用的妙用可以实现同步左子树和右子树的重量的作用。具体代码如下,易懂但思路难想,因为其特殊结构被引入到该文中。
示例代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| #include<iostream>
using namespace std;
bool solve(int & w)
{
int w1,l1,w2,l2;
cin >> w1 >> l1 >> w2 >> l2;
bool b1 = true,b2 = true;
if(w1==0) b1 = solve(w1);
if(w2==0) b2 = solve(w2);
w = w1 + w2;
return b1 && b2 && (w1*l1 == w2*l2);
}
int main()
{
int n;
cin >> n;
for(int i=1;i<=n;i++)
{
int w;
if(solve(w))
{
cout << "YES" << endl;
}
else
{
cout << "NO" << endl;
}
if(i!=n)
{
cout << endl;
}
}
return 0;
}
|

